
In the other cases, we follow the three-step recursive procedure we already described for disk 5. In this case we don't need to worry about smaller disks, so we can just move the disk directly. FUNCTION MoveTower disk, source, dest, spare): IF disk 0, THEN move disk from source to dest ELSE: MoveTower(disk-1, source, spare, dest) Step 1 above move disk from source to dest Step 2 above MoveTower(disk spare, dest, source) Step 3 above END IF Note that the pseudocode adds a base case: When disk is 0, the smallest disk.

Write a recurrence relation for the number of moves of the Hanoi Tower code Solve the. At the top level, we'll call MoveTower with disk 5, source dest B, and spares C. Question: Write a recursive pseudo code for Hanoi Tower problem. After we finish, we'll have disks 5 and smaller all on dest In pseudocode, this looks like the following. We do this recursively using the same procedure again. Finally, we want disks 4 and smaller moved from peg C (spare)to peg B (dest). Now, with all the smaller disks on the spare peg, we can move disk 5 from peg A (source)to peg B (dest) 3. (Bear with me if this doesn't make sense for the moment we'll do an example soon.) 2. nth disk at the bottom and 1st disk at the top. These disks are stacked over one other on one of the towers in descending order of their size from bottom i.e.
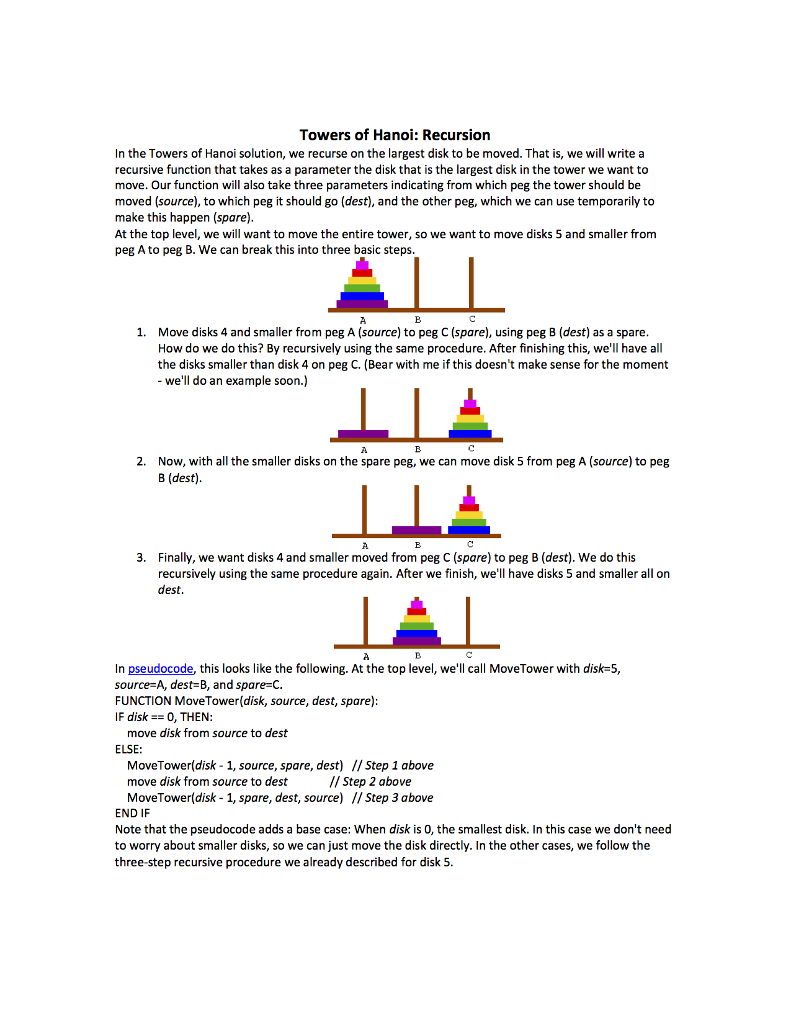
After finishing this, we'll have all the disks smaller than disk 4 on peg C. Tower of Hanoi is a mathematical puzzle which consists of three towers (or pegs) and n disks of different sizes, numbered from 1, the smallest disk, to n, the largest disk. How do we do this? By recursively using the same procedure. Move disks 4 and smaller from peg A (source) to peg C (spare), using peg B (dest) as a spare. We can break this into three basic steps.

At the top level, we will want to move the entire tower, so we want to move disks 5 and smaller from peg A to peg B. In one version of the puzzle Brahmin priests are completing the puzzle with 64 golden. This video is about an in depth look at one of the most challenging recursive problems for computer science students: Towers of Hanoi. So we now have a formula for the minimum moves with the Tower of Hanoi. Our function will also take three parameters indicating from which peg the tower should be moved (source), to which peg it should go (dest), and the other peg, which we can use temporarily to make this happen (spare). Can we see a pattern in the following list of minimum number of moves: 1,3,7,15,31,63, They are actually powers of 2 with one subtracted : 2 N-1. That is, we will write a recursive function that takes as a parameter the disk that is the largest disk in the tower we want to move. No disk may be placed on top of a smaller disk.Transcribed image text: Towers of Hanoi: Recursion In the Towers of Hanoi solution, we recurse on the largest disk to be moved.The previously mentioned tower with 100 disks would take approximately. Calculating the time needed for 64 disks, it will take more than 584.9 billion years, which is longer than the history of our known universe (approximately 13.8 billion years). a disk can only be moved if it is the uppermost disk on a stack. (2 n -1)÷31,536,000 time (in years) needed to complete a Tower of Hanoi with n disks. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack i.e. Search : Dfs Recursive Python Python Recursive Dfs Views: 1477 Published: Author: Search : table of content Part 1 Part 2 Part 3 Part 4 Part 5 Part 6 Part 7 Part 8 Part 9.The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules: A basic setup of Tower of Hanoi with 3 disks and 3 towers (often called rods) The disk all have different sizes as pictured above. Before we set the rules, let’s see how our universe looks like. Tower of Hanoi is a mathematical game, which has three rules.
Chegg code hanoi towers simulator#
The game is rather a simulator for the development of logical thinking, you can spend time playing at the same time doing. Step 1: Understand the Tower of Hanoi challenge. This game allows you not only to 'kill time', it is useful, corrupting logic.
Chegg code hanoi towers free#
The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top, thus making a conical shape. This version of the game is a test project of QasarApp, which means that it is distributed free of charge and without ads. It consists of three rods, and a number of disks of different sizes which can slide onto any rod. astar rrt path-planning potential-fields dijkstra-algorithm prm planning-algorithms local-planner probabilistic-road-map greedy-best-first-search.

The Tower of Hanoi (also called the Tower of Brahma or Lucas’ Tower, and sometimes pluralized) is a mathematical game or puzzle. An all-in-one application to visualize multiple different local path planning algorithms.


 0 kommentar(er)
0 kommentar(er)
